Définition
La base 10 ou décimale est la numération de position que nous utilisons en base dix dans la vie courante, on appelle ça une numération positionelle.
Dans ce type de codage, chaque nombre est représenté de façon unique par une suite ordonnée de chiffres. Et chaque chiffre représente une puissance de la base. Si on se limite dans un premier temps aux nombres entiers positifs, en base dix ces puissances sont : un (1), dix (représenté par 10), cent (dix fois dix, représenté par 100), mille (dix fois cent, représenté par 1000), dix mille etc.
Ce système est basé sur une logique à dix symboles, de 0 à 9, avec une unité supérieure (dizaine, centaine, etc.) à chaque fois que dix unités sont comptabilisées. C'est un système positionnel, c'est-à-dire que l'endroit où se trouve le symbole définit sa valeur. Ainsi, le 2 de 523 n'a pas la même valeur que le 2 de 132. En fait 523 est l'abréviation de 5·100+2·10+3. On peut selon ce principe imaginer une infinité de systèmes numériques fondés sur des bases différentes.
Historique
Nous avons vu avec Mr Delos, un enseignant de mathématiques, comment les anciennes civilisations comptaient et on a fait des exercices pour déchifrer leurs systèmes de calculs (par hyéroglyphes pour les Egyptiens par exemple)
La base dix est très ancienne. Elle découle d'un choix naturel, dicté- par le nombre des doigts des deux mains. Un système de notation décimale a été mis au point :
au IIIe millénaire av. J.-C., par les Égyptiens (le système égyptien était toutefois un système décimal sans positionnement) par exemple :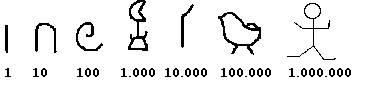
2000 ans avant notre ère par les sumériens :

Noter cependant l'usage de systèmes non décimaux, dont voici quelques exemples.
- Les anciennes civilisations de Mésopotamie (Sumer, Babylone…) utilisaient un système positionnel de base sexagésimale (60).
- À noter également l'usage de systèmes bisexagésimaux (binaire, décimal ou sexagésimal suivant la qualification des objets ou des êtres vivants à décompter).
- La civilisation maya utilisait un système de base 20 en introduisant quelques variantes.
- Le basque (ainsi que les langues celtiques) se fonde aussi sur la base 20. Il en reste quelques traces en français avec la dénomination « quatre-vingt ».
- Exemple de nombre en base dix (décimale)
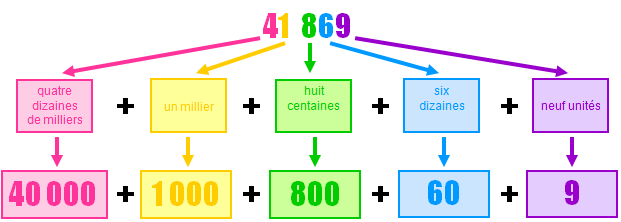
Mais comment écrire des chiffres et des nombres avec seulement le 0 et le 1 ?